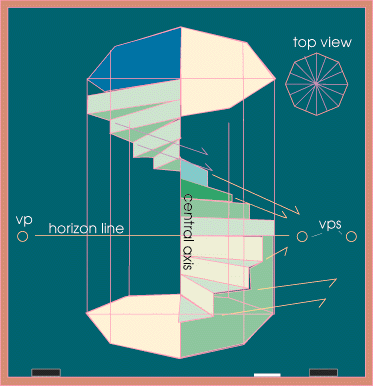Joe Sparano, a student from Omaha, asked about creating a spiral staircase using linear perspective. This process requires multiple vanishing points and the subdivision of a square. Generally speaking, we are constructing this in a cylinder, although my diagram uses an octagon. You will get the best understanding of the following explanation if you have read through the Chalkboard's pages on perspective drawing.

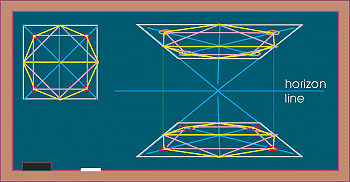
First one must establish where the horizon line will be since all convergences lines will recede to a number of vanishing points on this line. This will be at the viewer's eye level. Do this in one point perspective and assume that you are standing in front of these stairs at a 90 degree angle. Next, create an octagonal cylinder by subdividing a square. This can be done by dividing the square into fourths using crossing lines, then dividing again on the horizontal plane and crossing the center. Then one can cross center again while receding to the vanishing point. After this process, create a diamond by linking all the points where the horizontal and vertical lines meet the sides of the square. Once this has been done, you will find four points (indicated by red circles in the diagram below) that are halfway between the corners of the square and the sides of the diamond. By linking these points with the points of the diamond you will arrive at an octagon drawn in perspective (in the diagram there is another smaller square which is used to line up the points). Repeat this process to create the top of the "cylinder."

A spiral staircase uses a central axis from which all the steps radiate. One should establish the central axis and do all measurements from here. In the case of these stairs, the vertical measurement of each step would be done at this point. This is done because each step will be either protruding or receding from this central axis and will consequently change in relative size.

Once you have measured off equal distances on this vertical axis, you can begin to radiate lines out from this center. It is most accurate to repeat the octagon shape in perspective at each vertical increment to assure proper alignment. Once this has been done, only the edges of the stairs remain to be plotted.

The outside edges of the steps follow the same planes as those of the octagonal "cylinder." The vanishing point for each set of steps will change each time the plane changes. Notice that there are two steps for each plane, so there will be two steps receding to the same vanishing point. As the steps go back into space and rise the convergence lines change direction, but always recede to a point on the horizon line. Since we have eight sides on an octagon with four paralells, we will have four separate vanishing points.

This formula will change depending on the staircase that you have chosen. You can simplify by creating a spiral staircase in a square.

updated 07/16/04